In response to a Quora question, I wrote the following:
The reason why it is possible [to use faster-than-light travel to travel to the past] is that what appears as moving forward in time, faster than light, in one inertial frame appears as moving backward in time in another inertial frame.
Here is an example of a closed timelike loop that you can construct using FTL travel:
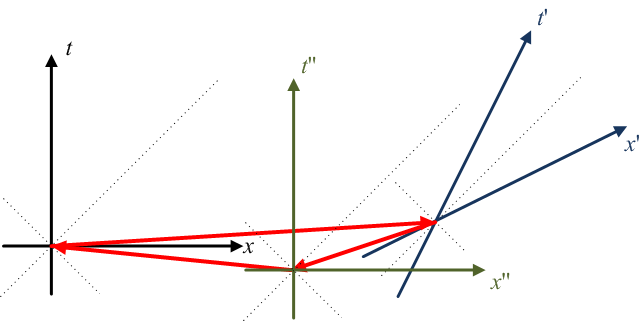
In this diagram, the journey (represented by the red arrows) begins on the left, moving FTL relative to the black, (t, x) inertial frame. Note that the traveler is moving forward in time in the (t, x) frame, but is actually moving backwards in time relative to the blue, (t', x') frame. The journey then continues from the right, moving FTL but forward in time relative to the (t', x') frame (but backwards in time relative to the (t, x) frame.) Finally, the last leg is moving FTL relative to the green, (t'', x'') frame (which is really just the (t, x) frame, translated; just trying to keep things simple.) The traveler arrives back at the point of his origin at the moment he left it, completing a closed timelike loop.
Of course if you have a preferred frame (say, the (t, x) frame in this diagram) and a rule that says that relative to that preferred frame, you can never move backwards in time, time travel may not be possible. But such a globally defined preferred frame may not even exist in spacetime curved by gravity.