Many novel ideas are found on the Internet. One not so novel notion is that Einstein was wrong and that the "lightspeed limit" is really just some international conspiracy of conservative "establishment" scientists. Those who make this point neglect the fact, however, that the deduction about the speed of light is not a result of some exotic assumptions or blind speculation, but a fairly simple consequence of some fundamental assumptions about nature: in other words, if you wish to prove that Einstein was wrong, you have to show that either elementary logic is incorrect, or that some of our basic assumptions about nature are outright false.
Here is why.
Symmetries in Nature
To begin, here are our assumptions, some of which are generic in nature, while others are specifically about electricity and magnetism. First, the generic ones:
- Space is homogeneous. The equations of physics work the same in New York and Los Angeles, on Earth or on Mars, in the Milky Way or in the Andromeda Galaxy.
- Space is isotropic. The equations of physics don't change just because you turn around and look in a different direction.
- Space is symmetric under time translation. The equations of physics are the same today as they were yesterday, and as they will be tomorrow and the day after that.
- Space is symmetric under a "boost". The equations of physics work the same in moving coordinate systems: your watch, computer, or your body for that matter won't cease to function just because you're moving on a train, an airplane, or spacecraft.
Maxwell's Equations
The specific assumptions about electricity and magnetism are the culmination of 100 years of research and experiment, and were first put into modern form by Maxwell in the 1860s. In plain English, this is what they say:
- The sum total of the electric field around a volume of space is proportional to the charges contained within.
- The sum total of the magnetic field around a volume of space is always zero, indicating that there are no magnetic charges (monopoles). (With a bar magnet, the number of field lines "going in" and those "going out" cancel each other out exactly, so there is no deficit that would show up as a net magnetic charge.)
- A change over time in the electric field or a movement of electric charges (current) induces a proportional vorticity in the magnetic field.
- A change over time in the magnetic field induces a proportional vorticity in the electric field, but in the opposite direction.
These four assumptions can also be stated exactly using mathematical language: specifically, the language of vector calculus. But before we continue, it is important to make note of the fact that we are done with the assumptions: what follows is rigorous logic. In other words, if one wishes to argue that Einstein's conclusion is wrong, one either has to throw logic out the window, or find fault in one or more of the assumptions above.
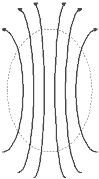 Empty Space
Empty Space
To examine the speed of light in free space, we can simplify two of our assumptions. In free space there are no charged bodies or particles about, and therefore Maxwell's first assumption reads as:
- The sum total of the electric field around a volume of empty space is zero, indicating there is no electric charge contained within.
Similarly, we can drop the bit about electric current from the third assumption:
- A change over time in the electric field in empty space induces a proportional vorticity in the magnetic field.
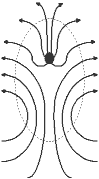 Divergence
Divergence
Mathematically, the first two assumptions are expressed through the concept of divergence. If we imagine the electric field with lines of force, as in a high-school physics textbook, divergence basically tells us how the lines are "spreading out". For the lines to spread out, there must be something, intuitively speaking, to "fill the gaps": these things would be particles of charge. But there are no such things in empty space, so we can say that the divergence of the electric field in empty space is identically zero:
\[{\rm div}~{\bf\mathrm{E}}=0.\]
The electric field is a vector field: the force it produces has a strength as well as a direction. The divergence of a vector field in a given coordinate system is computed through partial derivatives of the vector components:
\[{\rm div}~{\bf\mathrm{v}}=\frac{\partial v_x}{\partial x}+\frac{\partial v_y}{\partial y}+\frac{\partial v_z}{\partial z}.\]
So far so good. What we said about the electric field also applies to the magnetic field of course:
\[{\rm div}~{\bf\mathrm{B}}=0.\]
Vorticity
What about the vorticity? The vorticity of a vector field is also computed through partial derivatives:
\[{\rm curl}~{\bf\mathrm{v}}=\begin{pmatrix} \frac{\partial v_z}{\partial y}-\frac{\partial v_y}{\partial z}\\ \frac{\partial v_x}{\partial z}-\frac{\partial v_z}{\partial x}\\ \frac{\partial v_y}{\partial x}-\frac{\partial v_x}{\partial y}\end{pmatrix}.\]
Unlike the divergence of a vector field, which is a number field (called a scalar field), the vorticity of a vector field is another vector field. Intuitively what it means is that a vortex not only has strength, but it also has an axis pointing in a specific direction.
In this mathematical formalism, the second pair of Maxwell's equations in empty space can be expressed as:
\begin{align}{\rm curl}~{\bf\mathrm{B}}&=\epsilon_0\mu_0\partial{\bf\mathrm{E}}/\partial t,~~~{\rm and}\\ {\rm curl}~{\bf\mathrm{E}}&=-\partial{\bf\mathrm{B}}/\partial t,~~~~~\end{align}
where $\epsilon_0$ is the vacuum's electrical permittivity, $\mu_0$ its magnetic permeability.
To further simplify calculations, we'll assume that the field depends only on one spatial coordinate, say, \(x\). Feynman offers the example of a large (infinite?) charged sheet in the \(y\)-\(z\) plane that moves in a direction perpendicular to its surface as a source of this field. The same computation can be performed in the general case, but it is a lot more complicated (and a lot less instructive.)
Solution in One Spatial Dimension
In this case, the first pair of Maxwell's equations tells us that \(E_x\) and \(B_x\) must be constant functions.
The second pair of Maxwell's equations reduces to the following simple set:
\begin{align} -\frac{\partial B_z}{\partial x}&=\epsilon_0\mu_0\frac{\partial E_y}{\partial t},\\ \frac{\partial B_y}{\partial x}&=\epsilon_0\mu_0\frac{\partial E_z}{\partial t},\\ -\frac{\partial E_z}{\partial x}&=-\frac{\partial B_y}{\partial t},\\ \frac{\partial E_y}{\partial x}&=-\frac{\partial B_z}{\partial t}. \end{align}
Using the first and the fourth equation, for instance, we can find a solution for \(B_z\) (or \(E_y\)). Consider:
\[-\frac{\partial^2B_z}{\partial x^2}=\epsilon_0\mu_0\frac{\partial^2E_y}{\partial x \partial t},\]
and
\[\frac{\partial^2E_y}{\partial x \partial t}=-\frac{\partial^2B_z}{\partial t^2},\]
or
\[\epsilon_0\mu_0\frac{\partial^2B_z}{\partial t^2}-\frac{\partial^2B_z}{\partial x^2}=0.\]
This can be rewritten as:
\[\left(\sqrt{\epsilon_0\mu_0}\frac{\partial}{\partial t}-\frac{\partial}{\partial x}\right) \left(\sqrt{\epsilon_0\mu_0}\frac{\partial}{\partial t}+\frac{\partial}{\partial x}\right)B_z=0.\]
Solutions to this equation can be found in the form:
\[B_z=f_1(ct-x)+f_2(ct+x),\]
where \(f_1\) and \(f_2\) are arbitrary functions and $c=1/\sqrt{\epsilon_0\mu_0}$. The same solution exists for \(B_y\), \(E_y\), and \(E_z\).
If we set \(f_2=0\), then
\[B_z=f_1(ct-x),\]
which is a legitimate solution to Maxwell's equations. What this means is that if the field has a certain value at \(t=0\), \(x=0\), then it'll have the same value at \(t=t_0\), \(x=t_0\). Similarly, if we set \(f_1=0\), a field that has a certain value at \(t=0\), \(x=0\), then it'll have the same value at \(t=t_0\), \(x=-t_0\). Thus we can say that the electromagnetic field represented by this solution is moving at velocity $c$ along the \(x\) axis in either of two directions. The value of $c$ is observer independent, unless the properties of the vacuum ($\epsilon_0$ and $\mu_0$) are themselves dependent on the motion of the observer.
If, on the other hand, we assume that the vacuum is the same for all observers, the observed speed will be the same to all observers. Same regardless of where they are. Regardless of when they make their measurements. Regardless of how fast they themselves are moving, and in which direction they are facing. Whether you move towards a light source or away from it, the speed appears the same.
Special Relativity
This of course makes no sense in ordinary Euclidean spacetime: when you are running ahead of a moving train, it'll appear slower (i.e., take longer to hit you) than when you're running towards it.
Special relativity is simply the most economical way to solve this dilemma. The idea is to find the simplest geometry in which all our initial assumptions can be simultaneously true.
Why geometry? If you think about it, when you switch from a stationary coordinate system to a moving one (i.e., from a coordinate system fixed to the clock of a railway station to one that is fixed to the main axis of your steam engine) it's really just a simple coordinate transformation: \(t'=t\), \(x'=x-vt\). And herein lies the problem: after this coordinate transformation, in the new coordinate system a ray of light no longer satisfies the conditions that we derived previously. If, in the old coordinate system, an electromagnetic field had the same value at \(t=0\), \(x=0\) and \(t=t_0\), \(x=t_0\), in the new coordinate system, it'll have the same values at \(t'=0\), \(x'=0\) and \(t'=t_0\), \(x'=t_0-vt_0\), and this contradicts what we just learned about Maxwell's equations as \(x'\) won't be equal to \(t'\).
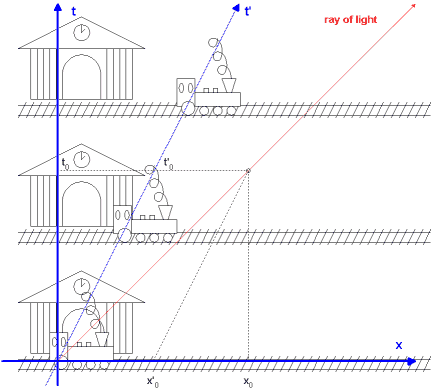
The simple geometry of special relativity, Minkowski spacetime, is built around the assumption that the quantity \(dt^2-dx^2-dy^2-dz^2\) remains constant under a "boost", i.e., when you change from one moving coordinate system to another. In our simple scenario with only one spatial coordinate, this reduces to \(dt^2-dx^2\) remaining constant when you switch from a stationary to a moving system. For rays of light moving in either direction, \(dt^2-dx^2\) remains 0 regardless whether you measure it from a moving or stationary system, which is precisely what we want in order to remain consistent with Maxwell's equations.
This assumption leads to a new form of coordinate transformation, the Lorentz transformation. To see why, compare the values for the station and the train in the diagram above. For the station, \(dt=t_0\), \(dx=x_0=vt_0\) (this, after all, is how we define the train's velocity \(v\)) and therefore, \(dt^2-dx^2\) is \(t_0^2-v^2t_0^2\). For the train, \(dx'=0\) and thus \((dt')^2-(dx')^2\) is \((t_0')^2\). We want the values for the station and the train to be equal:
\begin{align}(t_0')^2&=t_0^2-v^2t_0^2,\\ (t_0')^2&=t_0^2(1-v^2),\\ t_0'&=t_0\sqrt{1-v^2},\end{align}
and this, of course, is the fabled Lorentz transform.
Any other approach would either have to use a more complicated geometry (the late 19th century concept of "ether" can be viewed as an attempt to do just this) or it would require giving up at least some of our initial assumptions. And what's wrong with that, you ask? Well, those assumptions are supported by an enormous number of physical observations, not the least of which is the observation that this computer in front of me is functioning as expected, even though it is moving about at a not altogether inconsiderable velocity as the Earth spins, moves around the Sun and, along with the Sun, moves about in the Universe...
References
Feynman, Richard P., The Feynman Lectures on Physics II. (chapter 20), Addison-Wesley, 1977


