The problem of doing physics in curved spacetime can be stated simply. Most of physics concerns itself with differential equations. But ordinary derivative operators work only in the linear coordinate system of flat spacetime. So the question is whether a meaningful analog of the ordinary derivative operator can be invented that works in curved spacetime.
The answer comes in the form of a logical progression, which begins with generalizing a vector transformation law from ordinary rectangular coordinate systems to curvilinear ones; deriving the concept of covariance and contravariance and the notion of using infinitesimals as basis vectors; and then using these tools to derive a meaningful way to compare vectors in tangent spaces attached to different points of a spacetime. The result of this effort is the Christoffel-symbol, expressing the difference in the action of two derivative operators; armed with the Christoffel-symbol we can compute the difference between the derivative at a point in curved space relative to the ordinary derivative in a Euclidean tangent space at that point. The non-commutativity of this new derivative operator then offers a natural way to characterize curvature through the Riemann curvature tensor.
Vector Transformation Law
What is a vector? To the physicist, it is a quantity that has a magnitude and a direction. What a vector is not is a set of $n$ numbers. A set of $n$ numbers, at best, is the representation of a vector in a particular coordinate system, and may change as we change coordinate systems.
The first step in the analysis is to examine how, in a straight-line coordinate system, vector components are transformed under a linear transformation. As it is well known, so long as the origin remains in place the transformation can be fully described by a matrix:
\[{\vec{x}}'={\vec{A}}\cdot{\vec{x}},\]
or
Partial Derivatives
What we cannot do is to apply this method to anything other than straight-line coordinates in flat spacetime. Even something as simple as a polar coordinate system cannot be described this way. And, of course, we're in even deeper trouble in curved spacetime, where no straight-line coordinate system exists at all.
Now is the time to notice a simple identity. Since
the partial derivative of $x'_i$ with respect to $x_j$ shall be none other but the factor of $x_j$ in (2):
Of course when we stop using a straight-line coordinate system (even if we stay in a flat spacetime, e.g., when switching to polar coordinates) we can no longer use a constant transformation matrix with coefficients $a_{ij}$. But the following transformation law remains valid:
One way to look at this is to notice that the matrix coefficients now vary from one point to the next, as opposed to being the same constant matrix across all space.
Tensors, Covariant and Contravariant Quantities
In physics, one often deals with quantities that relate one vector to another, and are expressed in matrix form:
\[{\vec{y}}={\vec{T}}\cdot{\vec{x}}.\]
When we switch to another coordinate system, this is how this equation changes:
\[{\vec{y}}'={\vec{A}}\cdot{\vec{y}}={\vec{A}}\cdot{\vec{T}}\cdot{\vec{x}}.\]
How would we express $\vec{y}'$ as a function of $\vec{x}'$? Simple. First, we multiply on the left by $\vec{T}^{-1}\cdot\vec{A}^{-1}$ (remembering that matrix multiplication is not commutative, but it is associative):
\[{\vec{T}}^{-1}\cdot{\vec{A}}^{-1}\cdot{\vec{y}}'={\vec{T}}^{-1}\cdot{\vec{A}}^{-1}\cdot{\vec{A}}\cdot{\vec{T}}\cdot{\vec{x}}={\vec{x}}.\]
Next, we multiply on the left by $\vec{A}$:
\[{\vec{A}}\cdot{\vec{T}}^{-1}\cdot{\vec{A}}^{-1}\cdot{\vec{y}}'={\vec{A}}\cdot{\vec{x}}={\vec{x}}'.\]
Now that we have an expression with $\vec{x}'$ on the right hand side, all we need is to eliminate the factors of $\vec{y}'$ on the left side by multiplying both sides on the left with $\vec{A}\cdot\vec{T}\cdot\vec{A}^{-1}$:
\[{\vec{A}}\cdot{\vec{T}}\cdot{\vec{A}}^{-1}\cdot{\vec{A}}\cdot{\vec{T}}^{-1}\cdot{\vec{A}}^{-1}\cdot{\vec{y}}'={\vec{A}}\cdot{\vec{T}}\cdot{\vec{A}}^{-1}\cdot{\vec{x}}'.\]
Or, since matrix multiplication is associative:
This is the expression we sought, expressing $\vec{y}'$ as a function of $\vec{x}'$. Another way of looking at it is that we are, in effect, replacing $\vec{T}$ with $\vec{T}'=\vec{A}\cdot\vec{T}\cdot\vec{A}^{-1}$ as we switch to the new coordinate system
\[\begin{matrix} {\vec{x}}\Rightarrow{\vec{x}}'={\vec{A}}\cdot{\vec{x}},\\ {\vec{y}}\Rightarrow{\vec{y}}'={\vec{A}}\cdot{\vec{y}},\\ {\vec{T}}\Rightarrow{\vec{T}}'=({\vec{A}}\cdot{\vec{T}}\cdot{\vec{A}}^{-1}).\end{matrix}\]
A quantity like a vector that transforms according to the equation $\vec{x}'=\vec{A}^n\cdot\vec{x}$ (the exponent $n$ is a positive integer) is called contravariant. Specifically, a vector that transforms according to $\vec{x}'=\vec{A}\cdot\vec{x}$ is a contravariant vector. When $n\gt 1$, the quantity is a contravariant tensor (of type $n$).
A quantity that transforms according to the equation $\vec{x}'=\vec{x}\cdot\vec{A}^{-n}$ is a covariant quantity. A covariant vector is also often called a dual vector.
Tensors are often of a mixed type. The tensor $\vec{T}$ above is one example. Generally, a tensor that transforms according to $\vec{T}'=\vec{A}^k\cdot\vec{T}\cdot\vec{A}^{-l}$ is called a tensor of type $(k,l)$ with $k$ contravariant and $l$ covariant indices.
All tensors in fact form vector spaces; basic identities such as $a(\vec{U}+\vec{B})=a\vec{U}+a\vec{V}$ are true for any $a$ that is a real number and $\vec{U}$ and $\vec{V}$, which are tensors of the same type.
It is no accident that we expressed a linear relationship between vectors $\vec{x}$ and $\vec{y}$ above using a matrix $\vec{T}$. Generally, the following statement is true: Any linear relationship between a tensor $\vec{X}$ of type $(p,q)$ and a tensor $\vec{Y}$ of type $(r,s)$ can be expressed using a tensor $\vec{T}$ of type $(p+s,q+r)$. Specifically, in our case we expressed a linear relationship between two contravariant vectors (in other words, two tensors of type (1,0)), so the tensor we used was of type (1,1). Such a tensor is represented in a given coordinate system using a 2-dimensional matrix.
What are the components of the inverse matrix $\vec{A}^{-1}$? Rather than trying to compute the inverse matrix the hard way, it is instead expedient to examine what this matrix represents. Why, it of course tells us how we can obtain $\vec{x}$ from $\vec{x}'$:
\[{\vec{x}}={\vec{A}}^{-1}\cdot{\vec{A}}\cdot{\vec{x}}={\vec{A}}^{-1}\cdot{\vec{x}}'.\]
Using exactly the same argument used to derive (3), the components of $\vec{A}^{-1}$ can be seen as:
The transformation law for a tensorial quantity $\vec{T}$ of type $(k,l)$, expressed in component form, then becomes:
Good thing we have shorthand notation for this!
Abstract Index Notation
The abstract index notation was developed to make tensor equations simpler. First, one must realize that many tensor operations are independent of the basis. For instance, the exterior product of two contravariant vectors (upper indices are used to indicate a contravariant quantity):
\[T^{ab}=v^aw^b\]
appears, at first sight, to be dependent on the basis in which the components $v^a$ and $v^b$ are expressed. But, as can be verified by hand, the resulting product obeys the tensor transformation law:
\[T^{a'b'}=v'{}^{a'}w'{}^{b'},\]
and thus it is a tensorial quantity. Indeed, in the above expressions we don't really care what the coordinate system is in which the vectors or tensors are expressed in component form: the indices $a$ and $b$ are "abstract", all we need to know is whether two indices are the same, and whether two quantities are expressed using the same or different coordinates.
Yet another quantity that obeys the tensor transformation law is the interior, or tensor product. Multiplying a covariant (indicated by a subscripted index) and a contravariant vector's components and summing the result yields a scalar quantity that is independent of the coordinate system:
\[\sum\limits_av^a\omega_a=\sum\limits_{a'}v'^{a'}\omega_{a'}',\]
as can be verified through direct calculation.
To avoid having to use the summation sign too often, the Einstein summation convention is used. When an index appears in an expression twice, as a contravariant (upper) and covariant (lower) index, it is assumed that the expression will be summed over this index:
\[X^{a_1...c...a_n}_{b_1...c...b_k}=\sum\limits_cX^{a_1...c...a_n}_{b_1...c...b_k}.\]
Infinitesimal Quantities as Basis Vectors
At this point, it is important to notice a curious coincidence. There is another type of a "quantity" that transforms according to equation (6), this quantity being the operator $\partial/\partial x^i$. Given a real-valued smooth function $f$, its partial derivatives in the new coordinate system can be expressed as a function of its partial derivatives in the original system as a covariant quantity:
Similarly, an "infinitesimal displacement" $dx^i$ transforms as a contravariant quantity:
Because of this, the quantities $\partial/\partial x_i$ and $dx^i$ are often viewed, respectively, as the contravariant and covariant basis vectors in a given coordinate system. (And yes, there is more to this than that, but this article is not about differential forms.)
The whole point of this exercise, of course, is to develop a mechanism to deal with non straight-lined coordinate systems. Such coordinate systems exist in flat spacetime; one example is the polar coordinate system. What equation (7) tells us is how we can transform between arbitrary coordinate systems.
All this happened in flat space so far. But the mechanism that is described here is also applicable to converting between coordinate systems in curved space.
The Metric
Thanks to the work of a Greek chap named Pythagoras who lived some 2500 years ago, the distance between two points is easy to compute in a Cartesian coordinate system. This is not so in a non straight-lined coordinate system. However, by examining how the infinitesimal squared distance behaves under coordinate transformations, a meaningful new quantity can be derived.
In a Cartesian coordinate system, the infinitesimal squared distance is computed using the Pythagorean formula:
\[ds^2=\sum\limits_i(dx^{i})^2.\]
Under a change of coordinate systems, this quantity will transform as follows:
\[ds^2=\sum\limits_l\sum\limits_k\sum\limits_i\frac{\partial x_i'}{\partial x_k}\frac{\partial x_i'}{\partial x_l}dx^kdx^l.\]
By introducing the quantities
we can rewrite this formula as:
\[ds^2=\sum\limits_k\sum\limits_lg_{kl}dx^kdx^l.\]
Notice that:
\[\sum\limits_ig_{kl}dx^l=\frac{\partial}{\partial x_k}\sum\limits_k\sum\limits_lg_{kl}dx^kdx^l=\frac{\partial}{\partial x_k}ds^2.\]
If we take the infinitesimal square distance, $ds$, to be unity, what multiplying by $g_{kl}$ accomplished was a conversion from the infinitesimal quantity $dx^l$ to $\partial/\partial x_k$. This is called a "lowering of the index". What we basically find with the help of $g_{kl}$ is for any contravariant quantity a corresponding covariant quantity. This is true even for quantities with more than one index.
Similarly, the inverse of $g_{kl}$ can be used to "raise an index"; i.e., find the matching contravariant quantity for a covariant quantity.
The quantities $g_{kl}$ transform as a tensor of type (0,2). In other words, we discovered a tensorial quantity called the metric that exists independently of any specific coordinate system, provides us with information about infinitesimal squared distances, and helps us establish a correspondence between covariant and contravariant quantities. But is that all that the metric describes?
Christoffel Symbol
In a Euclidean space, it is possible to construct a parallel vector field: I.e., assigning the same vector to each point in space. Because of this, it also makes sense to talk about how a vector field changes from one point to the next; we can parallel-transport a vector from the first point to the second, and compare it with the value of the vector field there. Thus, the notion of a differential operator on a vector field is born.
The components of a parallel vector field are obviously constant relative to a rectangular coordinate system $x'^j$:
\[dX'{}^j=\sum\limits_k\frac{\partial X'{}^j}{\partial x'{}^k}dx'{}^k=0.\]
We can also express this displacement in a curvilinear coordinate system $x^j$. Using the identity $X'{}^j=\sum\limits_h(\partial x'{}^j/\partial x^h)X^h$ we get:
With the help of the metric, it is possible to eliminate the second derivatives from this equation. First, we need to differentiate the defining equation (10) with respect to $x^h$ and then cyclically permute the indices to obtain the following identities:
\[\frac{\partial g_{kl}}{\partial x^h}=\sum\limits_j\left(\frac{\partial^2x'{}^j}{\partial x^h\partial x^k}\frac{\partial x'{}^j}{\partial x^l}+\frac{\partial x'{}^j}{\partial x^k}\frac{\partial^2 x'{}^j}{\partial x^h\partial x^l}\right),\]
\[\frac{\partial g_{lh}}{\partial x^k}=\sum\limits_j\left(\frac{\partial^2x'{}^j}{\partial x^k\partial x^l}\frac{\partial x'{}^j}{\partial x^h}+\frac{\partial x'{}^j}{\partial x^l}\frac{\partial^2 x'{}^j}{\partial x^k\partial x^h}\right),\]
\[\frac{\partial g_{hk}}{\partial x^l}=\sum\limits_j\left(\frac{\partial^2x'{}^j}{\partial x^l\partial x^h}\frac{\partial x'{}^j}{\partial x^k}+\frac{\partial x'{}^j}{\partial x^h}\frac{\partial^2 x'{}^j}{\partial x^l\partial x^k}\right).\]
Adding the first and second of these equations, subtracting the third, and dividing by two we obtain:
We can now multiply (11) with $\partial x'{}^j/\partial x^l$ and sum over $j$, to get:
\[\sum\limits_j\frac{\partial x'{}^j}{\partial x^l}dX'{}^j=\sum\limits_hg_{hl}dX^h+\sum\limits_j\sum\limits_h\sum\limits_k\frac{\partial^2x'{}^j}{\partial x^h\partial x^k}\frac{\partial x'{}^j}{\partial x^l}X^hdx^k.\]
Substituting (12) we obtain the result we sought:
For a parallel vector field, (13) should be zero of course. The right hand side of this equation can then be made more meaningful if we multiply it by the inverse of $g_{hl}$. Yes, the metric has an inverse; otherwise, the coordinate system would become degenerate:
\[\sum\limits_lg^{jl}\sum\limits_hg_{hl}dX^h+\sum\limits_lg^{jl}\sum\limits_h\sum\limits_k\Gamma_{hkl}X^hdx^k=dX^j+\sum\limits_lg^{jl}\Gamma_{hkl}\sum\limits_h\sum\limits_kX^hdx^k=0.\]
Denoting $\sum_lg^{jl}\Gamma_{hkl}$ with $\Gamma_{hk}^j$, we get the following equation:
The quantities \(\Gamma_{hk}^j\) are called the Christoffel-symbols and they essentially express the difference between the ordinary differential operator of a rectilinear coordinate system and that of a curvilinear coordinate system. When the coordinate system is rectilinear and we perform a parallel transport, $dX^j$ is zero, and therefore \(\Gamma_{hk}^j\) is also zero. In a curvilinear coordinate system, we define parallel transport by equation (14); consequently, equation (14) also defines what can thereafter serve as a derivative operator.
When the space is intrinsically curved, there exists no rectilinear coordinate system of course, and straightforward differentiation is not possible. But, as any self-respecting physicist knows (much to the distress of self-respecting mathematicians) in a small enough neighborhood, everything is linear. What the Christoffel-symbols express, in this case, is essentially the differential operator of curved coordinates relative to the rectilinear coordinates of a Euclidean tangent space at a particular point. The main significance of the Christoffel-symbols lies in the fact that they provide a practical method for differentiation in curved space, by expressing the differential operator as a function of ordinary differential operators in a Euclidean tangent space.
Using equation (14), we can compute the differential of a contravariant vector field with respect to $x_k$:
\[D_kX^j=\frac{\partial X^j}{\partial x^k}+\Gamma_{hk}^jX^h.\]
If we were to repeat the same computation for a covariant vector field, we'd get a slightly different formula:
\[D_kX_j=\frac{\partial X_j}{\partial x^k}-\Gamma_{jk}^hX_h.\]
This method can be generalized to tensors of arbitrary type. For each contravariant index, one term will be added; for each covariant index, one term must be subtracted. Spelling it out, here's what we get:
\[D_kT^{j_1...j_r}_{i_1...i_s}=\frac{\partial T^{j_1...j_r}_{i_1...i_s}}{\partial x^k}+\sum\limits_{a=1}^r\Gamma_{mk}^{j_a}T_{i_1...i_s}^{j_1...j_{a-1}mj_{a+1}...j_r}-\sum\limits_{b=1}^s\Gamma_{i_bk}^mT_{i_1...i_{b-1}mi_{b+1}...i_s}^{j_1...j_r}.\]
Yuck. But, you get the idea.
Are we justified in calling $D_k$ a differential operator? Yes, for multiple reasons. First of all, $D_k$ has the common algebraic properties of a differential operator, namely bilinearity and the Leibniz rule. Furthermore, it can be shown that with respect to the metric, the choice of $D_k$ is unique: it is the only differential operator that preserves the inner product of two vectors as they are parallel-transported along any curve, i.e., $D_kg_{bc}v^bw^c=0$.
Commutators
It is interesting to take a look at the commutator of the derivative operator. In an ordinary rectilinear coordinate system the order in which differential operators are applied doesn't matter. In a curvilinear system, it does:
The commutator of the derivative operator with respect to a scalar field, i.e., \(\Gamma_{kl}^h-\Gamma_{lk}^h\), is called torsion. Often, the torsion is assumed to vanish for physically meaningful spacetimes, though this does not necessarily have to be the case.
Before proceeding any further, it ought to be mentioned that although it looks like one, \(\Gamma_{hk}^j\) is not really a tensor, as it depends on the choice of a coordinate system. Another way of looking at it is that it characterizes the differential operator in curved space relative to a particular coordinate system; if we used another coordinate system, we would derive a different \(\Gamma_{hk}^j\).
Curvature
We now have the rudiments of the apparatus need to express a fundamental geometric characteristic of curved space: its curvature. Intuitively, the notion is about the failure of a vector to remain parallel with itself as it is translated along a closed loop and returns to the origin. This can be seen easily as you imagine a north-pointing tangent vector at the Earth's equator. First, parallel transport this vector eastward ninety degrees. It'll still point towards the North Pole of course. Next, parallel transport the vector all the way to the North Pole. Finally, parallel transport it back to the point of origin, at which time you'll notice that the vector no longer points north; instead, it is now pointing west, along the equator.
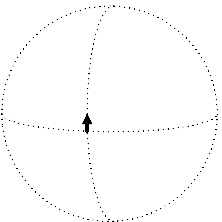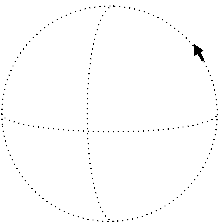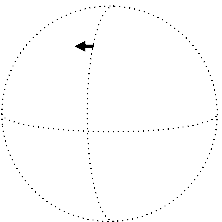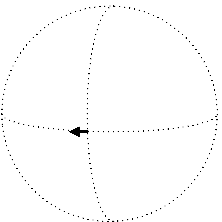
Of course we don't have to go all the way to the North Pole. We can simply cover a small rectangular area, going east first, then north, then back west and then south again, to return to the point of origin:
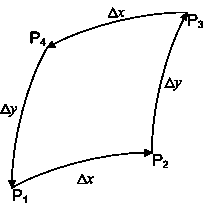
Changes to a vector $\vec{V}$ along the path $P_1P_2P_3$ can be expressed through the application of the appropriate differential operators. Denoting these as $D_x$ and $D_y$, we get $D\vec{V}=D_xD_Y\vec{V}$.
The path $P_3P_4P_1$ is but the path $P_1P_4P_3$ in reverse, which is to say that it can be expressed through the application of $D_y$ and $D_x$, in this order, and then multiplied by minus one.
Which means that the overall difference to a vector as it returns to the point of origin along the path $P_1P_2P_3P_4P_1$ can be computed using the expression $(D_yD_x-D_xD_y)\vec{V}$.
But this is none other than the commutator of the differential operator! This time, however, it has to be computed not for a scalar field, as we did in the previous section, but for a vector field.
In flat space, $D_xD_y-D_yD_x$ is, of course, zero. In other words, we're proposing to measure the curvature of space by determining how badly the differential operator fails to commute in that space when it is applied to a vector field.
Computing the commutator over a vector field is straightforward, though tedious:
\begin{align}D_l(D_kX^j)-D_k(D_lX^j)=&\frac{\partial}{\partial x^l}(D_kX^j)+\Gamma_{ml}^j(D_kX^m)-\Gamma_{kl}^m(D_mX^j)-\frac{\partial}{\partial x^k}(D_lX^j)\\
&{}-\Gamma_{mk}^j(D_lX^m)+\Gamma_{lk}^m(D_mX^j)\\
=&\left(\frac{\partial^2}{\partial x^l\partial x^k}-\frac{\partial^2}{\partial x^k\partial x^l}\right)X^j+\frac{\partial}{\partial x^l}(\Gamma_{hk}^jX^h)-\frac{\partial}{\partial x^k}(\Gamma_{hl}^jX^h)\\
&{}+\Gamma_{ml}^j\frac{\partial X^m}{\partial x^k}-\Gamma_{mk}^j\frac{\partial X^m}{\partial x^l}+\Gamma_{ml}^j\Gamma_{hk}^mX^h-\Gamma_{mk}^j\Gamma_{kl}^mX^h+(\Gamma_{lk}^m-\Gamma_{kl}^m)(D_mX^j)\\
=&\frac{\partial\Gamma_{hk}^j}{\partial x^l}X^h+\Gamma_{hk}^j\frac{\partial X^h}{\partial x^l}-\frac{\partial\Gamma_{hl}^j}{\partial x^k}X^h-\Gamma_{hl}^j\frac{\partial X^h}{\partial x^k}+\Gamma_{ml}^j\frac{\partial X^m}{\partial x^k}-\Gamma_{mk}^j\frac{\partial X^m}{\partial x^l}\\
&{}+\Gamma_{ml}^j\Gamma_{hk}^mX^h-\Gamma_{mk}^j\Gamma_{hl}^mX^h+(\Gamma_{lk}^m-\Gamma_{kl}^m)(D_mX^j)\\
=&\left(\frac{\partial\Gamma_{hk}^j}{\partial x^l}-\frac{\partial\Gamma_{hl}^j}{\partial x^k}+\Gamma_{ml}^j\Gamma_{hk}^m-\Gamma_{mk}^j\Gamma_{hl}^m\right)X^h+(\Gamma_{lk}^m-\Gamma_{kl}^m)(D_mX^j).\end{align}
The result consists of two parts, one of which we've already encountered: it is the torsion (15). The other part contains a tensor of type (1,3), which is called the Riemann curvature tensor:
When the torsion vanishes, i.e., when the spacetime is torsion-free, the curvature tensor (16) completely characterizes its intrinsic geometry.
Conclusion
At this point, we can conclude that three different quantities: the metric (10), the Christoffel-symbol (14), and the Riemann curvature tensor (16), all express the same thing: the geometry of a spacetime as seen by denizens of that spacetime (i.e., the intrinsic curvature.) If you have the metric, you can determine the Christoffel-symbol for the preferred derivative operator. With the Christoffel-symbol at hand, you can compute the curvature tensor. If all you have is the curvature tensor, you can derive the metric.
In practice, knowing the Christoffel-symbol is the most important, since it is these symbols that give a straightforward prescription for differentiation. With the derivative operator thus "tamed", one can proceed and try to express ordinary physical equations, for instance Maxwell's equations of the electromagnetic field, in curved spacetime and start doing some real physics with it!
References
| Lovelock, David & Rund, Hanno, Tensors, Differential Forms, and Variational Principles, Dover Publications, 1989 |
| Wald, Robert M., General Relativity, The University of Chicago Press, 1984 |


