Computer Algebra System
Several years ago, I became one of the developers of the open-source computer algebra system (CAS) called Maxima.
Maxima is the open source descendant of the first ever computer algebra system, MACSYMA. Initially developed by the US Department of Defense, it was later commercialized. The company behind commercial MACSYMA has since disappeared, but in the late 1990s, the DOE agreed to permit the original version to be released under an open-source license.
My interest in Maxima is due to my interest in general relativity. Perhaps more than most other areas of physics, general relativity relies heavily on computer algebra tools, due to the complexity involved with defining and analyzing metrics in curved spacetime.
Maxima has two packages related to general relativity work. They both perform complicated tensor calculations. One package, itensor, is a general-purpose package that deals with indexed objects: specifically, objects with covariant, contravariant, and derivative indices. The package knows about contraction rules, the raising and the lowering of indices, ordinary and covariant differentiation, and Christoffel symbols. The other package, ctensor, is really a collection of subroutines that are designed to compute tensor components used mainly in general relativity, including the components of the Christoffel symbols, the Riemann tensor, the Ricci tensor, and the Weyl tensor. The two packages neatly complement each other: many problems can be solved by writing up and deriving indicial tensor equations using itensor, and then using a special function provided by the itensor package to convert the result into component form that can then be processed by ctensor.
The main problem with the tensor packages was, simply put, that they were broken! This is where I come in: having been able to fix the core functionality in itensor, I decided to offer my services to the Maxima development team.
I'm working on more than mere fixes, however. I have also extended the functionality of the tensor packages. On the one hand, I improved the algebraic power of itensor, introducing a new notation that helps preserve index ordering in more complicated tensor equations. On the other hand, I added to both ctensor and itensor the capability to deal with not just the standard metric formalism, but also with rigid frames, torsion, and conformal nonmetricity. Time permitting, I'd also like to add more capabilities in the future, to make Maxima "competitive" with other well-known tensor packages, such as SHEEP, CLASSI, and grTensorII.
Meanwhile, I added a third tensor package: atensor is a package that can deal with generalized (tensor) algebras, including Clifford, Grassmann, and Lie-algebras. I also fixed the cartan package, a package that deals with with differential forms. Last but not least, I changed these four packages so that their naming conventions now conform to that of commercial MACSYMA.
I have drafted a paper that summarizes the work I've done. For additional reference, here's a link to the tensor package manuals (snapshot from the current development version of Maxima) and some demos:
- Algebraic tensor manipulation (atensor)
- Component tensor manipulation (ctensor)
- Indicial tensor manipulation (itensor)
- Tensor package demos (text output, ~370 kB; as of March, 2008)
The following are two more complete examples that demonstrate some of the new capabilities that I added to these packages:
The Kaluza-Klein metric
In 1919, Theodor Kaluza proposed an extension to general relativity: using an appropriately constructed fifth dimension, he was able to incorporate electromagnetism into Einstein's theory of gravity. Recently, I endeavored to replicate the most basic of Kaluza's results: the equation of motion for a particle in empty five-dimensional space, as seen from a four-dimensional perspective.
Now that I am working with Maxima, the question arose: can the same result be reproduced using this computer algebra system? Surprisingly, the answer is a yes. With only minor changes to the current Maxima code base, I was able to complete the derivation.
The Petrov classification
One of the common problems in general relativity is determining the equivalence of two metrics. Because the same manifold can be mapped using drastically different coordinate systems, it is usually not at all evident whether or not two metrics describe the same manifold. A set of routines that I am working on make it possible to derive the Petrov class for a metric specified using an orthonormal tetrad base.
Differentiation with respect to field variables
The newest addition (March 2008) to Maxima is the ability to differentiate indexed expressions with respect to indexed variables, most notably the metric. This feature makes it possible to use Maxima to derive the Euler-Lagrange equations from a field Lagrangian; indeed, Maxima can now deduce the field equations of general relativity from the Einstein-Hilbert action, and also can deal with other theories based on a modified Lagrangian, such as Brans-Dicke theory.
The power of the package can now be demonstrated by showing how Maxima, starting from the Lagrangian density of the gravitational field (the Einstein-Hilbert Lagrangian) can derive, and solve, the field equations in the spherically symmetric case, a plot of the celebrated Schwarzschild gravity well. In other words, starting with
\[{\cal L}=\frac{1}{16\pi G}(R+2\Lambda)\sqrt{-g},\]
and running the following code:
if get('ctensor,'version)=false then load(ctensor);
if get('itensor,'version)=false then load(itensor);
remsym(g,2,0);
remsym(g,0,2);
remsym(gg,2,0);
remsym(gg,0,2);
remcomps(gg);
imetric(gg);
icurvature([a,b,c],[e])*gg([d,e],[])$
contract(rename(expand(%)))$
%,ichr2$
contract(rename(expand(%)))$
canform(%)$
contract(rename(expand(%)))$
components(gg([a,b],[]),kdels([a,b],[u,v])*g([u,v],[])/2);
components(gg([],[a,b]),kdels([u,v],[a,b])*g([],[u,v])/2);
%th(4),gg$
contract(rename(expand(%)))$
contract(canform(%))$
imetric(g);
contract(rename(expand(%th(2))))$
remcomps(R);
components(R([a,b,c,d],[]),%th(2));
g([],[a,b])*R([a,b,c,d])*g([],[c,d])$
contract(rename(canform(%)))$
contract(rename(canform(%)))$
components(R([],[]),%);
decsym(g,2,0,[sym(all)],[]);
decsym(g,0,2,[],[sym(all)]);
ishow(1/(16*%pi*G)*((2*L+'R([],[])))*sqrt(-determinant(g)))$
L0:%,R$
canform(contract(canform(rename(contract(expand(diff(L0,g([],[m,n]))-
idiff(diff(L0,g([],[m,n],k)),k)+idiff(rename(idiff(contract(
diff(L0,g([],[m,n],k,l))),k),1000),l)))))))$
ishow(e([m,n],[])=canform(%*16*%pi/sqrt(-determinant(g))))$
EQ:ic_convert(%)$
ct_coords:[t,r,u,v];
lg:ident(4);
lg[2,2]:-a^2/(1-k*r^2);
lg[3,3]:-a^2*r^2;
lg[4,4]:-a^2*r^2*sin(u)^2;
dependencies(a(t));
cmetric();
derivabbrev:true;
christof(false);
e:zeromatrix(4,4);
ev(EQ);
expand(radcan(ug.e));
lg:ident(4);
lg[1,1]:B;
lg[2,2]:-A;
lg[3,3]:-r^2;
lg[4,4]:-r^2*sin(u)^2;
kill(dependencies);
dependencies(A(r),B(r));
cmetric();
christof(false);
e:zeromatrix(4,4);
ev(EQ);
E:expand(radcan(ug.e));
exp:findde(E,2);
solve(ode2(exp[1],A,r),A);
%,%c=-2*M;
a:%[1],%c=-2*M;
ode2(ev(exp[2],a),B,r);
b:ev(%,%c=rhs(solve(rhs(%)*rhs(a)=1,%c)[1]));
factor(ev(ev(exp[3],a,b),diff));
lg:ev(lg,a,b),L=0$
ug:invert(lg)$
block([title: "Schwarzschild Potential for Mass M=2",M:2.],
plot3d([r*cos(th),r*sin(th),1-ug[1,1]],[r,5.,50.],[th,-%pi,%pi],
['grid,20,30],['z,-2,0],[psfile],['legend,title]));
we end up with this plot:
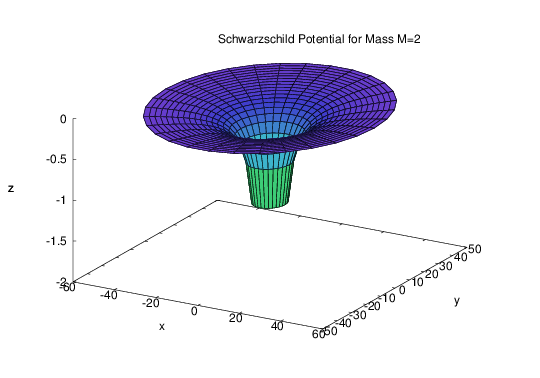
I believe this capability is unique to the Maxima tensor package.