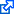Hardware Construction
 Beware of programmers who carry screwdrivers. - Leonard Brandwein
Beware of programmers who carry screwdrivers. - Leonard Brandwein
I've been a software guy all my life. However, I was always fascinated by electronics, and part of my success as a programmer was due to my thorough understanding of how computers work.
Back in 1999, I put that understanding to the ultimate test: I actually designed, and built, a simple but functional 4-bit computer from low-level electronic components (TTL logic gates.) Although this machine has less than one tenth of a percent of the speed and one millionth of the memory of a modern Pentium system, not to mention that its "user interface" is just a set of miniature switches and blinking LED lights, I still consider this a proud accomplishment.
If you are interested, you can study a full description of this system, including logic diagrams and more. Or, if you just want an overview, here's a photo and, to demonstrate the programming model of this processor, a small program that multiplies two 4-bit numbers to obtain an 8-bit result:
00: F CLF ; Initialize 01: 7 0 0 AND 00 ; Load 0 to accumulator 04: 2 E F STA FE ; Set #FE to 0 07: 1 C F LDA FC ; Load first argument 0A: 5 F 0 AND 0F ; Take low nybble 0D: 2 A F STA FA ; Store at working storage 10: 1 D F LDA FD ; Load second argument 13: 5 F 0 AND 0F ; Take low nybble 16: 2 9 2 STA 29 ; Store as argument to ADD instruction 19: 1 A F LDA FA ; Load first argument 1C: F CLF ; 1D: E ROR ; Take one bit 1E: 2 A F STA FA ; Store the rest 21: C E 2 JNC 2E ; If not 1, no need to add 24: 1 E F LDA FE ; Load result 27: F CLF ; 28: 7 0 0 ADD 00 ; Add second argument (stored here) 2B: 2 E F STA FE ; Store result 2E: 1 9 2 LDA 29 ; Load second argument 31: F CLF ; Multiply by 2 32: D ROL ; 33: 2 9 2 STA 29 ; Store 36: 1 A F LDA FA ; Reload first 39: F CLF ; 3C: 7 0 0 ADD 00 ; Check for 0 3D: 9 D 1 JNZ 1D ; Repeat loop if necessary 40: 0 HLT ; Result obtained 41: 3 0 0 JMP 00 ; Restart FA: 0 0 ; Working storage FC: 3 5 ; Operands FE: 0 0 ; Result
Complex floating point algorithms, such as that of the Gamma function (my favorite programming example for programmable calculators) are probably forever beyond the capabilities of this beast; you're not going to implement a floating point library in a mere 256 nybbles! It is, however, possible to implement a simple factorial program, and surprisingly, it doesn't even require the use of a multiplication subroutine. It makes efficient use of repeated additions instead. This implementation calculates an 8-bit result, so the highest number it accepts as its argument is 5, but it still demonstrates a neat solution. After entering the program, its argument must also be entered at address FE-FF; the 1-byte (2-nybble) result can be read from FC-FD.
00: 1 E F LDA FE ; Move FE to FC (argument in FE) 03: 2 C F STA FC 06: 1 C F L1: LDA FC ; Move FC to 35 09: 2 5 3 STA L5+1 0C: 1 E F LDA FE ; Decrement FE 0F: F CLF 10: 8 1 0 SUB 01 13: 9 A 1 JNZ L3 ; If FE==0 END 16: 0 HLT ; (result is in FC) 17: 3 6 1 L0: JMP L0 1A: 2 E F L3: STA FE 1D: 2 A F STA FA ; Move FE to FA 20: 1 A F L2: LDA FA ; Decrement FA 23: F CLF 24: 8 1 0 SUB 01 27: 9 D 2 JNZ L4 ; If FA==0 goto L1 2A: 3 6 0 JMP L1 2D: 2 A F L4: STA FA 30: 1 C F LDA FC ; FC=FC+35 33: F CLF 34: 7 0 0 L5: ADD 00 37: 2 C F STA FC 3A: 3 0 2 JMP L2 ; LOOP
Disclaimer: I built this processor as a hobby project, as a means of self-education to learn more about hardware architectures. The ideas and inventions used here are my own, but it is entirely possible that some of the solutions have been used by others elsewhere, and are protected by patents. If you plan to utilize any of the solutions disclosed herein for a commercial purpose, you are advised to do the necessary research to ensure that your product or service does not violate an in-force patent in your country. Needless to say, this disclaimer does not free you from the obligation to observe my copyright prior to republishing my work in whole or in part, or otherwise utilizing it for a commercial purpose.