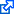Research Application
In the early 2000's, I wrote software code to process and recover telemetry data from archived raw telemetry files obtained from the Pioneer 10 and 11 spacecraft between 1972 and 2003. This led to my participation in the investigation of the Pioneer Anomaly, an as-yet unexplained small, anomalous acceleration of these two spacecraft that was measured as the spacecraft were leaving the Solar System. Over the years, I developed a precision orbit determination program (ODP) that can model spacecraft orbits and radio-metric tracking data with the necessary accuracy. I also developed some thermal modeling code, as part of our investigation of the possibility that much (all?) of the anomaly is due to the recoil force caused by heat radiated by the spacecraft in an anisotropic pattern.
Pioneer 10 and 11 were launched in 1972 and 1973, respectively. These were humanity's first two spacecraft to leave the inner solar system, cross the asteroid belt, and make close-up observations of the gas giang Jupiter. The missions were tremendously successful. Both spacecraft reached Jupiter safely, providing the first ever close-up observations of the planet, its moons, and its immense radiation fields. Pioneer 11 used Jupiter's gravity for a maneuver that took it across the solar system, for an eventual encounter with Saturn several years later. The two spacecraft continued to operate well beyond their original design lifetime: Pioneer 11 was last contacted in 1995, whereas Pioneer 10's last transmission was received in 2003.
The Pioneer 10 and 11 spacecraft were spin-stabilized. The spacecraft's axis of rotation coincided with their antenna axis, and was oriented in the direction of the Earth. Infrequent precession maneuvers were needed to ensure that the Earth remained within the antenna beamwidth. This meant that much of the time, the spacecraft flew completely undisturbed. As a result, Pioneer 10 and 11 remains the most precise large-scale gravitational experiment to date and for the foreseeable future.
In the 1990s, it became apparent, however, that in order to achieve maximum agreement between theory and data, the theory needed to be modified. This small correction was in the form of a constant sunward acceleration, with an approximate magnitude of $a_P=(8.74\pm 1.33)\times 10^{-10}~{\rm m}/{\rm s}^2$.
My first contribution to researching the Pioneer anomaly was a C++ software library that could process Master Data Records, a format used by NASA's DSN (Deep Space Network) to store raw Pioneer telemetry.
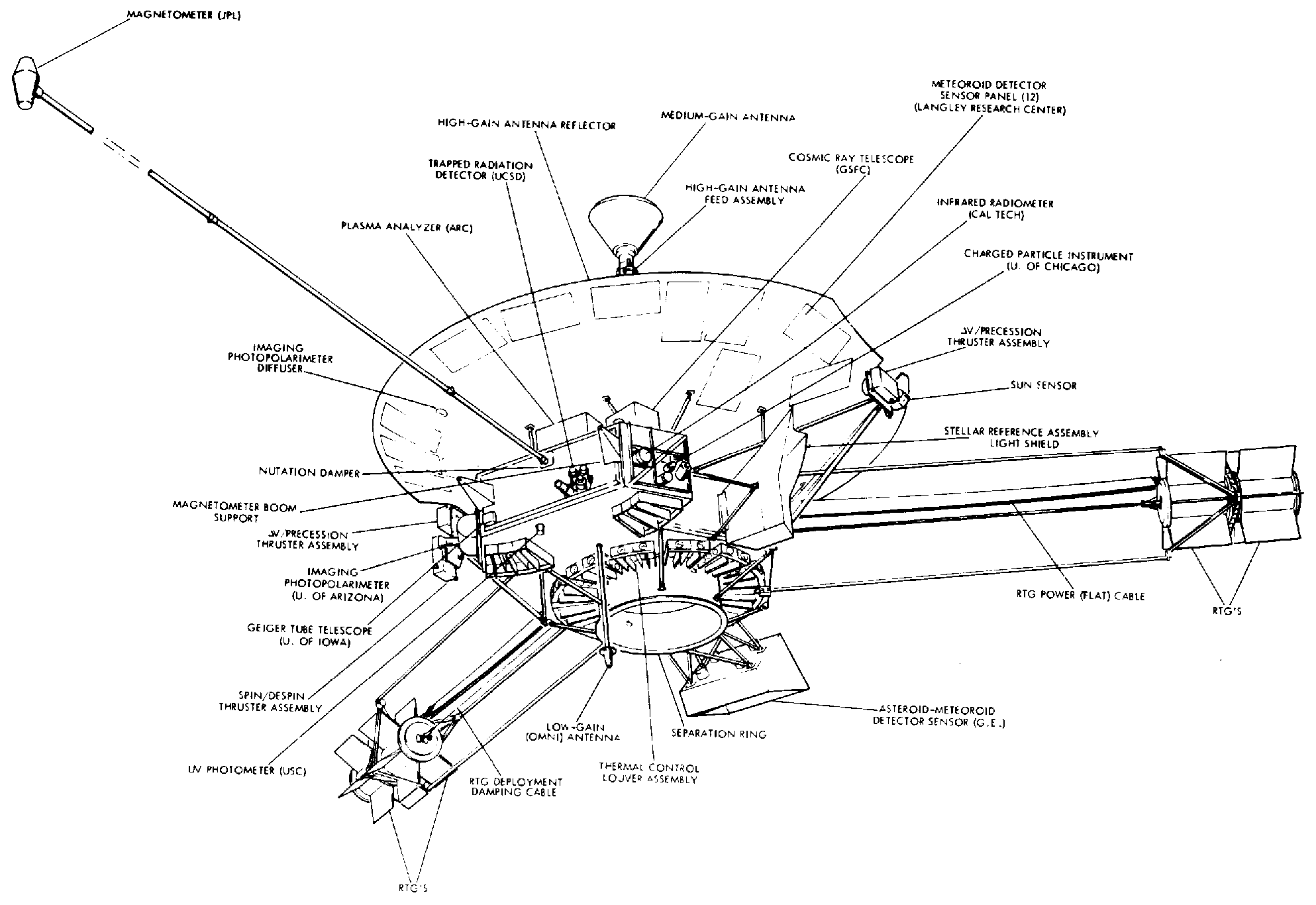
Subsequently, I developed a full-blown orbit determination program that could utilize DSN radio-metric Doppler measurements of the Pioneer radio signal to model the Pioneer spacecraft orbits with high precision. The program can be run from the command line, but I also developed a Windows front-end using Visual C++ that made it easier to investigate test cases and monitor the calculation.
The program solves the relativistic equations of motion
\[\frac{d^2\vec{r}}{dt^2}=\frac{\mu_i}{|\vec{r}_i-\vec{r}|^3}(A_i(\vec{r}_i-\vec{r})+\vec{B}_i),\]
where $\vec{r}$ is the spacecraft's position, $\vec{r}_i$ is the position, $\mu_i$ is the mass of the $i$-th solar system body, $t$ is the time and the post-Newtonian correction terms $A_i$ and $\vec{B}_i$ are given by
\begin{align}A_i&=1-\frac{1}{c^2}\left\{2(\beta+\gamma)\sum\limits_j\frac{\mu_j}{|\vec{r}_j-\vec{r}|}+\gamma v^2+(1+\gamma)v_i^2-2(1+\gamma)\vec{v}\cdot\vec{v}_i-\frac{3}{2}\left[\frac{(\vec{r}-\vec{r}_i)\cdot\vec{v}_i}{|\vec{r}_i-\vec{r}|}\right]^2\right\},\\
\vec{B}_i&=\frac{1}{c^2}\left\{(\vec{r}-\vec{r}_i)\cdot\left[(2+2\gamma)\vec{v}-(1+2\gamma)\vec{v}_i\right]\right\}(\vec{v}-\vec{v}_i).\end{align}
The parameters $\beta$ and $\gamma$ are the so-called Eddington-parameters; they are both 1 for general relativity, but may have different values for alternate theories of gravity.
The software also models the effects of the oblateness of Jupiter and Saturn (these become important when the spacecraft is near these giant planets) as well as the propagation of the radio signal through the solar system, affected by gravity, charged particles from the Sun, and the Earth's atmosphere. The positions of solar system bodies and the precise locations of DSN ground stations are obtained from NASA data sets. Nongravitational forces, notably solar pressure, are also accounted for by the code.
Uniquely, my program can also model the recoil force due to on-board generated heat that is radiated in an anisotropic pattern. Most of the heat on-board is due to two sources: waste heat from the spacecraft's radioisotope thermoelectric generators (RTGs) and electrical heat. It turns out that the thermal recoil force $\vec{F}_\mathrm{recoil}$ is proportional to a linear combination of the power $Q_\mathrm{rtg}$ and $Q_\mathrm{elec}$ of these two heat sources:
\[\vec{F}_\mathrm{recoil}\propto \eta_\mathrm{rtg}Q_\mathrm{rtg}+\eta_\mathrm{elec}Q_\mathrm{elec},\]
where the two coefficients $\eta_\mathrm{rtg}$ and $\eta_\mathrm{elec}$ are yet to be determined. To estimate the magnitude of these coefficients, and to verify that it is indeed legitimate to model the thermal recoil force this way, I also developed a finite element model of the spacecraft that, in combination with a raytracing algorithm, estimated $\eta_\mathrm{rtg}$ and $\eta_\mathrm{elec}$.
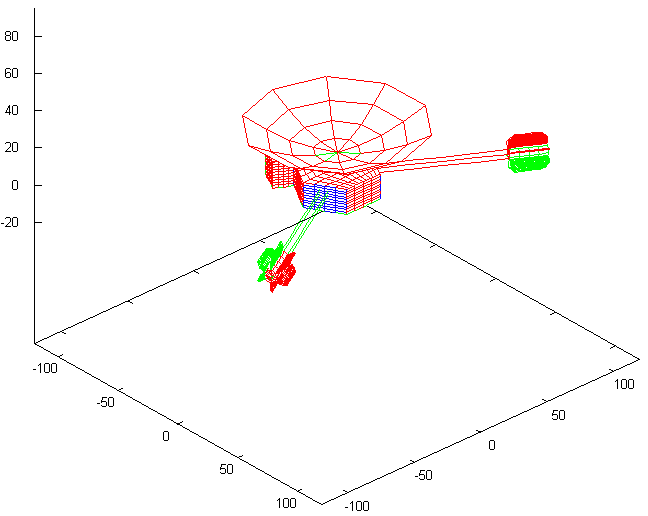
I first developed a finite element model of the spacecraft using Maxima. In turn, the Maxima code that I wrote generated C++ code which was then utilized by a generic raytracing algorithm that I developed. The final program ran from the command line as it iteratively estimated the thermal output of the spacecraft. One version of the program could also estimate the resulting change in angular momentum (due to the way heat is reflected off some asymmetric spacecraft components, thermal radiation could also affect the spacecraft's rotation, and indeed, an anomalous change in the rotation rate of both spacecraft was detected.)
This research is still on-going. Earlier in 2011, I gave a seminar at the Perimeter Institute, detailing some interim results. More results being reported as they become available.