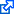This page contains a JavaScript calculator of Hawking radiation and other parameters of a Schwarzschild black hole.
The original idea belongs to Jim Wisniewski, whose page from 2006 (link) appears to be no longer available available again, but since it is not archived by the Wayback Machine, I think my functional clone is still useful.
Wisniewski's original code included a fictitious unit of mass, the "standard industrial neuble", equivalent to a billion metric tons, from Will McCarthy's novel The Collapsium. I kept the unit, but decided to use instead the much more useful value of one solar mass as the initial mass.
As in Wisniewski's version, specifying any quantity causes the others to be recalculated accordingly (see source). The drop-down menus select the units of measure to be used for their corresponding input field.
An added feature is the calculation of the "peak photon" wavelength, corresponding frequency, and photon energy, representing the peak of the blackbody radiation curve per unit logarithm (of wavelength or frequency) that corresponds to the black hole temperature. The latest version also correctly accounts for the black hole's effective area, light scattering, and the resulting change in its evaporation lifetime.
| Quantity | Value | Units | Expression |
|---|---|---|---|
| Mass | $M$ | ||
| Schwarzschild radius | $R = M \dfrac{2G}{c^2}$ | ||
| Surface area | $A = M^2 \dfrac{16 \pi G^2}{c^4}$ | ||
| Effective density | $\rho = \dfrac{1}{M^2}\dfrac{3c^6}{32\pi G^3}$ | ||
| Surface gravity* | $\kappa = \dfrac{1}{M} \dfrac{c^4}{4G}$ | ||
| Surface tides | $d\kappa_R = \dfrac{1}{M^2}\dfrac{c^6}{4G^2}$ | ||
| Time to singularity | $t_S = M\dfrac{\pi G}{c^3}$ | ||
| Entropy | (dimensionless) | $S = M^2 \dfrac{4\pi G }{\hbar c}$ | |
| Temperature | $T = \dfrac{1}{M}\dfrac{\hbar c^3}{8\pi k_BG}$ | ||
| Peak photons | $\lambda_{\rm logpeak} = M \dfrac{16\pi^2 G}{c^2[W(-4e^{-4})+4]}$ | ||
| Nominal luminosity | $L = \dfrac{1}{M^2}\dfrac{\hbar c^6}{15360\pi G^2}$ | ||
| Lifetime | $t = M^3 \dfrac{5120\pi G^2}{1.8083\hbar c^4}$ |
*The surface gravity calculated here is the Newtonian value. The actual surface gravity is infinite at the horizon; that is to say, an infinitely powerful rocket would be needed for an object to maintain its position precisely at the event horizon.
Discussion
Wisniewski started his calculations with the standard formula for the Schwarzschild radius of a mass $M:$
$$R = \frac{2G}{c^2}M$$
As per [Hawking 1974], the thermodynamic temperature of such a black hole is
$$T = \frac{\kappa}{2\pi} = \frac{\hbar c^3}{8\pi k_BG}\frac{1}{M}.$$
Its surface area is
$$A = 4\pi R^2 = \frac{16\pi G^2}{c^4} M^2,$$
making the Hawking radiation luminosity at least ((the actual figure, as discussed below, is about 1.6 times this value):
$$L = A\sigma T^4 = \frac{\hbar c^6}{15360\pi G^2 }\frac{1}{M^2}.$$
Peak photons are calculated using Planck's radiation law:
$$B_\nu(\nu,T)=\frac{2h\nu^3}{c^2}\frac{1}{e^{h\nu/k_BT}-1},$$
where $\nu$ is the frequency. Alternatively, we can express it as a function of wavelength, $\lambda=c/\nu:$
$$B_\lambda(\lambda,T)=B_\nu(\nu,T)\frac{d\nu}{d\lambda}=\frac{2hc^2}{\lambda^5}\frac{1}{e^{hc/\lambda k_BT}-1}.$$
The derivatives of both these equations can be solved for in closed form using Lambert's W-function, but the peak frequency and peak wavelength will not coincide. However, when we reexpress $B$ in terms of either $\log\nu$ or $\log\lambda,$ a consistent solution is obtained:
$$\lambda_{\rm logpeak}=\dfrac{hc}{k_BT[{\rm W}(-4e^{-4})+4]}.$$
The dimensionless Bekenstein-Hawking entropy of the black hole is defined by
$$S = \frac{c^3A}{4G\hbar}=M^2\frac{4\pi G}{\hbar c}.$$
Multiply this value by the Boltzmann constant $k_B$ to get the entropy in conventional units.
At a distance $r$ from a black hole with mass $M$, the incident radiation flux is, therefore,
$$\Phi = \frac{L}{4\pi r^2} = \frac{\hbar c^6}{61440\pi^2 G^2r^2}\frac{1}{M^2} .$$
The amount of radiation actually intercepted by an object necessarily depends upon its exposed area.
The free-fall time $t_S$ from horizon to singularity is calculated as
$$t_s=\frac{1}{c}\int\frac{1}{\sqrt{\dfrac{2GM}{c^2r}-1}}~dr=\frac{\pi GM}{c^3}\simeq \frac{M}{M_\odot}\times 1.54\times 10^{-5}~{\rm s}.$$
The expression for $L$ makes it possible to calculate the lifetime of a black hole of given initial mass $M_0$, assuming no mass input. Luminosity means energy output, thus
$$-\frac{dE}{dt} = \frac{\hbar c^6}{15360\pi G^2}\frac{1}{M^2}.$$
Since $dE = dM c^2$,
$$-\frac{dM}{dt} = \frac{\hbar c^4}{15360 \pi G^2}\frac{1}{M^2}.$$
Separating variables and integrating, we obtain
$$t = \frac{5120\pi G^2}{1.8083\hbar c^4} M^3,$$
where we also introduced the numerical factor of 1.8083. It comes from detailed calculations in [Page 2005]*, and arises as a combination of effects. First, the effective absorbing (hence, emitting) surface area of the black hole is much larger, $\tfrac{27}{4}$ times larger in fact than the $4\pi R^2$ area corresponding to the event horizon. This would result in a large (factor of 6.75) increase, but it is mitigated by the fact that not all light rays that enter the photon sphere are in fact captured by the black hole's event horizon. Consequently, photons are emitted at a rate that is 1.6232 times in excess of the "naive" calculation. Additionally, we must also consider gravitons: these are emitted at 0.1851 times the "naive" rate. Combined, these two terms give the overall factor of 1.8083. (Page also considered neutrinos, but unless at least one neutrino flavor is massless, they will not contribute except near the very end of the evaporation process when the black hole becomes quite hot.)
Plugging in the various constants, this works out to
$$t = \left(\frac{M}{M_\odot}\right)^3 \times 1.160 \times 10^{67}{\rm yr},$$
where $M_\odot=1.989\times 10^{30}~{\rm kg}$.
The lifetime of a $1~M_\odot$ black hole, therefore, is calculated as nearly 57 orders of magnitude longer than the present age of the universe. But that does not take into account the fact that such a black hole is colder than the cosmic microwave background radiation bathing it. Therefore, whatever little energy it radiates, it actually receives more in the form of heat from the cosmos. So rather than shrinking, it would continue to grow. Indeed, any black hole with a mass greater than about 0.75% of the Earth's mass is colder than the cosmic background, and thus its mass increases for now. As the universe expands and cools, however, eventually the black hole may begin to lose mass-energy through Hawking radiation.
*I thank Stephen Selipsky for bringing Page's results to my attention and for his patient explanations.