Simply put, the principle of least action is about finding the "cheapest" route between two points in space-time.
How do you measure "cheapest"? If all you measure is the distance, the "cheapest" is a straight line, but often, going in a straight line is not practical. When you try to get across a mountain, for instance, the straight line may mean years of tunnel-boring. The next best thing, a straight line on the map, would require climbing over the mountain, so you might conclude that the "cheapest", in this case, is going around it.
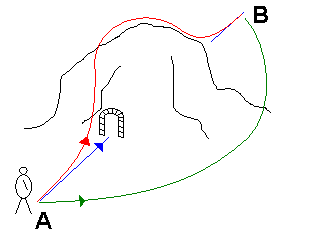
This is what the principle of least action is all about: the "cheapest" route as a function of some measure of "cost".
How can we compute the "cheapest" route? We first must observe that if a given route is the cheapest, then neighboring routes will necessarily be more expensive, no matter how we vary the route. So we denote the cost by $S$ and the route by $\rho$. What happens when we vary the route, keeping the endpoints fixed? What we get is $S(\rho+\eta)=S+\epsilon_S$. Since $S$ is expected to be minimal when $\eta=0$, $\eta$ itself must be zero in the first order; otherwise, its rate of change would be proportional to the rate of change of some coordinate, so if we vary that coordinate in the opposite direction, $\epsilon_S$ would become negative, contradicting the assumption that $S$ was to be minimal.
Sounds like a trivial problem in differential calculus, but there's a catch: $\eta$ is not a number, but an arbitrary function assigned to different paths between the endpoints.
As a practical example, I recently tried to derive the equation of motion for an electrically charged particle in an electrostatic field. The "cost", more commonly called the action, of such a particle is known to be:
\[S=-m\int\sqrt{1-v^2}~dt-q\int[\phi(t,r,\theta)-\vec{v}.\vec{A}(t,r,\theta)]~dt,\]
where $\phi$ and $\vec{A}$ are the electromagnetic scalar and vector potentials, respectively, $r$ and $\theta$ are polar coordinates, and $v$ is the particle's velocity. (How this relativistic action is derived goes beyond the scope of this article, but the bottom line is this: the first term really is the action associated with a "straight line", and the second term is known from experience to correctly represent the contributions of the electromagnetic field.)
First of all, I'm assuming that $\vec{A}=0$, i.e., there's no magnetic field. The action integral then reduces to:
\[S=-m\int\sqrt{1-v^2}~dt-q\int\phi(t,r,\theta)~dt.\]
The expression for $v$ of course is $v=\sqrt{(dr/dt)^2+r^2(d\theta/dt)^2}$. Varying $r$ by $\epsilon$ and dropping terms higher-order in $\epsilon$, I get:
\begin{align}\delta\sqrt{1-v^2}&=\delta\sqrt{1-\left(\frac{dr}{dt}\right)^2-r^2\left(\frac{d\theta}{dt}\right)^2}\\
&=\sqrt{1-\left(\frac{dr}{dt}+\frac{d\epsilon}{dt}\right)^2-(r+\epsilon)^2\left(\frac{d\theta}{dt}\right)^2}-\sqrt{1-v^2}\\
&=\sqrt{1-\left(\frac{dr}{dt}\right)^2-2\frac{dr}{dt}\frac{d\epsilon}{dt}-\left(\frac{d\epsilon}{dt}\right)^2+(r^2+2r\epsilon+\epsilon^2)\left(\frac{d\theta}{dt}\right)^2}-\sqrt{1-v^2}\\
&=\sqrt{1-\left(\frac{dr}{dt}\right)^2-2\frac{dr}{dt}\frac{d\epsilon}{dt}-(r^2+2r\epsilon)\left(\frac{d\theta}{dt}\right)^2}-\sqrt{1-v^2}\\
&=\sqrt{1-v^2-2\left[\frac{dr}{dt}\frac{d\epsilon}{dt}-r\epsilon\left(\frac{d\theta}{dt}\right)^2\right]}-\sqrt{1-v^2}\\
&=\sqrt{\left\{\sqrt{1-v^2}-\frac{1}{\sqrt{1-v^2}}\left[\frac{dr}{dt}\frac{d\epsilon}{dt}-r\epsilon\left(\frac{d\theta}{dt}\right)^2\right]\right\}^2}-\sqrt{1-v^2}\\
&=\sqrt{1-v^2}-\frac{1}{\sqrt{1-v^2}}\left[\frac{dr}{dt}\frac{d\epsilon}{dt}-r\epsilon\left(\frac{d\theta}{dt}\right)^2\right]-\sqrt{1-v^2}\\
&=-\frac{1}{\sqrt{1-v^2}}\left[\frac{dr}{dt}\frac{d\epsilon}{dt}-r\epsilon\left(\frac{d\theta}{dt}\right)^2\right].\end{align}
Now I can put this back into the equation for $S$:
\begin{align}S'&=-\int m\sqrt{1-v^2}-\frac{m}{\sqrt{1-v^2}}\left[\frac{dr}{dt}\frac{d\epsilon}{dt}+r\epsilon\left(\frac{d\theta}{dt}\right)^2\right]+q\phi+q\epsilon\frac{\partial\phi}{\partial r}dt\\
&=S+\int\frac{m}{\sqrt{1-v^2}}\left[\frac{dr}{dt}\frac{d\epsilon}{dt}+r\epsilon\left(\frac{d\theta}{dt}\right)^2\right]-q\epsilon\frac{\partial\phi}{\partial r}dt.\end{align}
Similarly, if I vary $\theta$ by $\epsilon$ and drop terms higher-order in $\epsilon$, I get:
\begin{align}S''=-\int m\sqrt{1-v^2}-\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}\frac{d\epsilon}{dt}+q\phi+q\epsilon\frac{\partial\phi}{\partial\theta}dt\\
=S+\int\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}\frac{d\epsilon}{dt}-q\epsilon\frac{\partial\phi}{\partial\theta}dt.\end{align}
Feynman's old trick is to eliminate the terms containing $d\epsilon/dt$ by integrating in parts:
\[\int f\frac{d\epsilon}{dt}dt=f\epsilon-\int\frac{df}{dt}\epsilon dt.\]
Now is the time to remember that we're really computing a definite integral between the two endpoints, and $\epsilon$ is null at the endpoints, so the $f\epsilon$ bit will vanish. Therefore, We're left with:
\[S'=S+\int\epsilon\left[\frac{m}{\sqrt{1-v^2}}r\left(\frac{d\theta}{dt}\right)^2-\frac{d}{dt}\left(\frac{m}{\sqrt{1-v^2}}\frac{dr}{dt}\right)-q\frac{\partial\phi}{\partial r}\right]dt,\]
and
\[S''-S-\int\epsilon\left[\frac{d}{dt}\left(\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}\right)+q\frac{\partial\phi}{\partial\theta}\right]dt.\]
Assuming that $\phi$ represents a central force field, we can observe that $\partial\phi/\partial\theta$, is going to be identically zero:
\[S''=S-\int\epsilon\frac{d}{dt}\left(\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}\right)dt.\]
Since $\epsilon$ can be an arbitrary function, in order for the integrals to be zero (which is what we want, as per the action principle) the factor of $\epsilon$ must be zero. First we deal with the equation for $S''$, which implies:
\begin{align}\frac{d}{dt}\left(\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}\right)&=0,\\
\frac{mr^2}{\sqrt{1-v^2}}\frac{d\theta}{dt}&=C,\\
\frac{m}{\sqrt{1-v^2}}&=\frac{C}{r^2\frac{d\theta}{dt}}.\end{align}
Substituting this into the equation for $S'$, we get:
\[C^2\frac{\sqrt{1-v^2}}{mr^3}-\frac{d}{dt}\left(\frac{C}{r^2\frac{d\theta}{dt}}\frac{dr}{dt}\right)-q\frac{\partial\phi}{\partial r}=0.\]
which simplifies as:
\begin{align}\frac{C^2\sqrt{1-v^2}}{mr^3}-\frac{d}{dt}\left(\frac{C}{r^2}\frac{dr}{d\theta}\right)-q\frac{\partial\phi}{\partial r}&=0,\\
\frac{C^2\sqrt{1-v^2}}{mr^3}-\frac{d}{dt}\left(\frac{C}{r^2}\right)\frac{dr}{d\theta}-\frac{C}{r^2}\frac{d^2r}{d\theta dt}-q\frac{\partial\phi}{\partial r}&=0,\\
\frac{C^2\sqrt{1-v^2}}{mr^3}-\frac{d}{dt}\left(\frac{C}{r^2}\right)\frac{dr}{dt}\frac{dr}{d\theta}-\frac{C}{r^2}\frac{d^2r}{d\theta dt}-q\frac{\partial\phi}{\partial r}&=0,\\
\frac{C^2\sqrt{1-v^2}}{mr^3}+\frac{2C}{r^3}\frac{dr}{dt}\frac{dr}{d\theta}-\frac{C}{r^2}\frac{d^2r}{d\theta dt}-q\frac{\partial\phi}{\partial r}&=0,\end{align}
but
\[\frac{dr}{dt}=\frac{dr}{d\theta}\frac{d\theta}{dt}=\frac{dr}{d\theta}\frac{C\sqrt{1-v^2}}{mr^2},\]
so the equation reduces to
\[\frac{C^2\sqrt{1-v^2}}{mr^3}+\frac{2C}{r^3}\frac{C\sqrt{1-v^2}}{mr^2}\left(\frac{dr}{d\theta}\right)^2-\frac{C}{r^2}\frac{d}{d\theta}\left(\frac{dr}{d\theta}\frac{C\sqrt{1-v^2}}{mr^2}\right)-q\frac{\partial\phi}{\partial r}=0.\]
One nasty derivative remains:
\[\frac{d}{d\theta}\left(\frac{dr}{d\theta}\frac{C\sqrt{1-v^2}}{mr^2}\right)=\frac{d^2r}{d\theta^2}\frac{C\sqrt{1-v^2}}{mr^2}+\frac{dr}{d\theta}\frac{d}{d\theta}\frac{C\sqrt{1-v^2}}{mr^2},\]
however
\[\frac{C\sqrt{1-v^2}}{mr^2}=\frac{d\theta}{dt},\]
and thus the second term reduces to $d^2\theta/d\theta dt$, i.e., the angular acceleration. When $v\ll 1$, this will be a small value, so it can be ignored. Which leaves us with the equation
\[\frac{C^2\sqrt{1-v^2}}{mr^3}+\frac{2C}{r^3}\frac{C\sqrt{1-v^2}}{mr^2}\left(\frac{dr}{d\theta}\right)^2-\frac{C}{r^2}\frac{d^2r}{d\theta^2}\frac{C\sqrt{1-v^2}}{mr^2}-q\frac{d\phi}{dr}=0.\]
Rearranging a little, we get:
\[\frac{C^2\sqrt{1-v^2}}{mr}+\frac{2C^2\sqrt{1-v^2}}{mr^3}\left(\frac{dr}{d\theta}\right)^2-\frac{C^2\sqrt{1-v^2}}{mr^2}\frac{d^2r}{d\theta^2}-qr^2\frac{d\phi}{dr}=0.\]
Or, after substituting $\phi=1/r$, the scalar potential of an electrical charge:
\begin{align}\frac{C^2\sqrt{1-v^2}}{mr^2}\frac{d^2r}{d\theta^2}-\frac{2C^2\sqrt{1-v^2}}{mr^3}\left(\frac{dr}{d\theta}\right)^2&=\frac{C^2\sqrt{1-v^2}}{mr}+q,\\
\frac{d^2r}{d\theta^2}-\frac{2}{r}\left(\frac{dr}{d\theta}\right)^2&=r+\frac{qmr^2}{C^2\sqrt{1-v^2}}.\end{align}
Once again making the assumption that $v\ll 1$, i.e., $\sqrt{1-v^2}=1$, this equation can be solved easily:
| \[\frac{1}{r}=-\frac{qm}{C^2}+C_1\sin\theta+C_2\cos\theta.\] |
This is the equation of a conic section, like an ellipse or a hyperbole, using polar coordinates $r$ and $\theta$. The actual shape depends on the charge ($q$), mass ($m$), the coupling constant ($C$), and the two constants ($C_1$ and $C_2$) that represent initial conditions.
I don't know how to solve this problem without the non-relativistic simplifications. I played a little with Maple, and obtained some solutions. The results are somewhat encouraging: although it is hard to see through the tangled mess of integration constants, it appears that what I got is indeed approximately periodic, with a precession constant of $\sqrt{1-q^2/C^2}$. This seems consistent with the standard result in Landau's and Lifshitz's tome.
References
Feynman, Richard P., The Feynman Lectures on Physics II. (chapter 19), Addison-Wesley, 1977


